Ressources - OSU Pythéas

Ressources

Océan

Pression HyperBAR fait sa pause estivale… rendez-vous le 16 septembre pour une nouvelle saison !

by

Depuis plusieurs années, Pression HyperBAR ! propose un format convivial permettant le dialogue entre scientifiques et citoyens. Chaque soirée débute par de courtes interventions permettant de poser les bases du sujet avant de laisser une large place aux questions, aux échanges et aux débats, le tout dans une ambiance conviviale autour d’un verre de la Brasserie Zoumaï à Marseille.

Cette soirée sera présentée par les étudiants du Master ISME (Information Scientifique et Médiation en Environnement) d’Aix Marseille Université. Dans le cadre de leur formation, ils relèveront le défi d’animer cette soirée, sur une thématique scientifique et sociétale d’actualité !

Les premiers rendez vous de la rentrée auront pour thèmes :

  • Mercredi 16 septembre, la soirée sera consacrée au concept d’« Une seule santé ! »
  • Mercredi 7 octobre, nous aborderons la thématique « biodiversité et énergies renouvelables »

Que vous soyez passionnés de sciences, curieux des grands enjeux environnementaux ou simplement désireux de mieux comprendre le monde qui nous entoure, ces rendez-vous sont ouverts à toutes et à tous, sans inscription.

Pression HyperBAR ! c’est un mercredi par mois, de 19 h à 21 h, à la Brasserie Zoumaï, 7 cours Gouffé, 13006 Marseille.

Alors, profitez de l’été… et pensez dès maintenant à noter cette date dans votre agenda !

Evaluer les effets du changement climatique et des pressions anthropiques grâce au suivi des communautés planctoniques

by

Partant du constat que le plancton, composante essentielle des réseaux trophiques marins et des cycles biogéochimiques, est souvent étudié de manière fragmentée, l’objectif a été de développer une vision globale de sa biodiversité et des facteurs qui contrôlent sa distribution. Les résultats révèlent une forte diversité couvrant l’ensemble du continuum planctonique, des microorganismes au zooplancton. Les niveaux de diversité les plus élevés sont observés dans les fractions de petite taille, tandis que les fractions supérieures à 64 µm sont dominées par les métazoaires, notamment les Arthropodes. Les échantillons collectés par bouteilles Niskin présentent une forte abondance de protistes tels que les Syndiniales et les Rhizaires. Le métabarcoding met également en évidence de nombreux taxons rares ou cryptiques, dont certains parasites microscopiques difficilement détectables par les méthodes traditionnelles.

L’étude montre que la structure des communautés est principalement déterminée par la profondeur, la taille des organismes et la résolution taxonomique considérée. Des gradients spatiaux marqués distinguent les zones côtières, plus riches en nutriments, des régions océaniques oligotrophes. La température, la stratification de la colonne d’eau et la disponibilité en nutriments apparaissent comme les principaux facteurs environnementaux contrôlant cette organisation. Cette approche intégrée et FAIR souligne la complémentarité des données d’imagerie et des outils moléculaires, et constitue une base essentielle pour renforcer la surveillance des écosystèmes méditerranéens et mieux comprendre leur réponse aux changements climatiques et aux pressions anthropiques.

Au-delà, elle confirme l’intérêt de l’existence d’un observatoire pérenne tel que MOOSE pour réaliser un portrait intégré de la biodiversité planctonique en Méditerranée.

Cartographier la frontière entre la lumière du Soleil et la bioluminescence en Méditerranée grâce aux planeurs sous-marins

by

Une équipe de chercheurs d’Aix Marseille Université et du CNRS a mis en évidence, pour la première fois en Méditerranée, la profondeur à laquelle la lumière produite par les organismes marins devient plus importante que la lumière d’origine atmosphérique. Cette étude, menée dans le cadre du projet BIOLUMOPS (BIOLUminescence Marine, Observations spatio-temporelles in situ par Planeur Sous-marin, financé par l’Agence Innovation Défense) ouvre de nouvelles perspectives sur les paysages lumineux sous-marins et leur influence sur les écosystèmes marins.

Pour réaliser ces observations, les scientifiques ont pu s’appuyer sur l’expertise du laboratoire MIO (Institut Méditerranéen d’Océanologie), du shom (Service hydrographique et océanographique de la Marine) et de l’entreprise ALSEAMAR pour déployer des planeurs sous-marins autonomes, « gliders » équipés de capteurs mesurant à la fois la lumière solaire pénétrant dans l’océan et la bioluminescence émise par plus des ¾ des organismes marins. « Les gliders ont transformé l’océanographie moderne en offrant une plateforme autonome capable d’emporter des capteurs scientifiques sur de longues durées, là où les navires ne peuvent observer que de façon ponctuelle » Nagib Bhairy, co-auteur de l’étude en charge de la planification, du déploiement et du pilotage des gliders.

Les campagnes, réalisées dans le golfe du Lion au printemps et à l’été 2025, ont permis de collecter des données jusqu’à 600 mètres de profondeur, profondeur limitante d’un capteur. Les résultats des analyses de ces données menées par Andrea Hay, en post-doctorat au MIO, montrent que cette « profondeur de transition bioluminescente » varie fortement au cours de la journée. Autour de midi, elle se situe entre 250 et 450 mètres de profondeur, alors qu’à minuit la bioluminescence peut dominer jusqu’à proximité de la surface. Cette dynamique reflète l’équilibre permanent entre l’atténuation de la lumière solaire dans l’eau et l’activité lumineuse des organismes marins.

« Au-delà de la performance technologique, cette découverte apporte un nouvel éclairage sur le rôle écologique de la lumière dans l’océan. La bioluminescence constitue en effet un moyen essentiel de communication, de défense ou de prédation pour de nombreuses espèces marines. Identifier les zones où elle devient visible par rapport à la lumière ambiante permet de mieux comprendre les comportements des organismes et l’organisation verticale des communautés marines au cours du temps », ajoute Séverine Martini, spécialiste de la bioluminescence et porteuse du projet BIOLUMOPS. Cette étude démontre également le potentiel des planeurs sous-marins pour observer à haute résolution des phénomènes biologiques encore peu documentés. À l’heure où les paysages lumineux océaniques évoluent sous l’effet des changements environnementaux, ces nouvelles observations constituent un outil précieux pour mieux comprendre le fonctionnement et l’évolution des écosystèmes marins.

Le dégel des sols arctiques ne réveille qu’une partie des microbes

by

Au Svalbard, un archipel isolé de l’Arctique situé entre la Norvège continentale et le pôle Nord, les sols restent gelés pendant la majeure partie de l’année. Ces environnements froids, pauvres en nutriments et largement dépourvus de végétation renferment pourtant d’importantes quantités de carbone piégé dans le pergélisol.

Avec le réchauffement rapide de l’Arctique, ces sols dégèlent désormais pendant des périodes plus longues chaque été. Une nouvelle étude montre que ce dégel n’entraîne pas une activation complète de la vie microbienne. En réalité, environ la moitié des micro-organismes présents dans ces sols restent dormants, même après plusieurs mois de dégel.

Suivre la reprise de l’activité microbienne
Malgré leur apparence austère, les sols arctiques abritent des communautés microbiennes diversifiées qui jouent un rôle clé dans la régulation des émissions de carbone vers l’atmosphère. Lorsque le sol dégèle, l’eau liquide devient disponible, permettant aux micro-organismes de reprendre leur activité.

Pour mieux comprendre ce processus, une équipe internationale incluant des scientifiques du CNRS à l’Institut Méditerranéen d’Océanologie (MIO) a incubé des sols du Svalbard et suivi directement la croissance microbienne grâce à une technique de marquage isotopique de l’ADN. Cette approche a permis d’identifier précisément quels micro-organismes se développaient après le dégel.

Les résultats montrent que certains micro-organismes s’activent rapidement, tandis que d’autres ne commencent à croître qu’après plusieurs semaines. Une grande partie de la communauté reste toutefois inactive.

Ce travail a été réalisé dans le cadre du projet ERC SIESTA, qui vise à mieux comprendre le rôle de la dormance microbienne dans des environnements extrêmes.

Au-delà de la décomposition : des interactions biologiques clés
De manière inattendue, les micro-organismes actifs ne se limitent pas aux décomposeurs de matière organique. L’étude met également en évidence la croissance de bactéries prédatrices, capables de consommer d’autres micro-organismes. Ce résultat souligne que les interactions au sein des réseaux trophiques microbiens jouent un rôle important dans le fonctionnement des sols arctiques après le dégel.

Un enjeu majeur pour le climat
Les sols arctiques stockent environ un tiers du carbone des sols mondiaux. Avec l’accélération du réchauffement, le devenir de ce carbone dépend étroitement de l’activité microbienne.

Cette étude montre que les émissions de carbone ne sont pas uniquement contrôlées par la température, mais aussi par l’identité des micro-organismes qui deviennent actifs, et le moment auquel ils s’activent. Ces résultats suggèrent que les modèles climatiques actuels pourraient simplifier excessivement la réponse des sols arctiques au réchauffement.

Exposition « Sous l’horizon » dans le cadre des extatiques

by

Premier rendez-vous de la saison culturelle Les Extatiques de Paris La Défense dont la direction artistique a été confiée à COAL pour la saison 2026-2027, l’exposition « Sous l’Horizon » invite à une immersion dans les mondes invisibles de l’océan. Dans un espace de 1000 mètres carrés, habituellement inaccessible au public situé sous la Grande Arche, les visiteurs équipés d’un casque audio et d’une lampe torche, traversent un parcours poétique et sensoriel, mêlant science et fiction. Avec les œuvres d’Antoine Bertin, Jérémie Brugidou, Ugo Schiavi et Shivay La Multiple ; et les mots de Mariette Navarro contés par Emily Loizeau.

Du 3 au 26 avril 2026.

 

Tout au long de la saison, une constellation d’expériences singulières viendra rythmer la programmation. Intitulées Sociétés secrètes, ces propositions invitent le public à explorer autrement les trésors artistiques et patrimoniaux du territoire, et à vivre des rencontres rares, parfois inattendues.

Les Sociétés secrètes incarnent pleinement l’esprit de la saison D’autres Mondes : offrir des expériences capables de déplacer les regards et de transformer notre perception du vivant, de l’espace et du collectif. Chaque rendez-vous devient une porte d’entrée vers des réalités parallèles, discrètes mais agissantes.

Conçues comme des moments insolites et immersifs, ces rencontres prennent des formes variées — activations artistiques, rituels imaginaires, explorations urbaines… Elles esquissent l’existence d’usages inédits, d’autres mondes et d’autres futurs possibles, qui s’inventent en silence sous nos pas et révèlent la pluralité des mondes qui coexistent autour de nous.

Billetterie Les Extatiques – Sous l’horizon : réservez vos billets pour l’exposition dès maintenant et choisissez votre créneau en ligne.

 

Deux rendez-vous de bar des sciences en collaboration avec l’OSU Pythéas !

Jeudi 9 avril — Rencontre avec la bioluminescence

  • 18h30 – 19h | Apéro-quiz Océan

Un temps convivial et participatif animé par la Fondation de la Mer pour tester ses connaissances sur les mystères du vivant marin

  • 19h – 20h | Discussion croisée animée par Sophie Bécherel

Une soirée consacrée à la bioluminescence, phénomène biologique par lequel certains micro-organismes marins produisent de la lumière grâce à des réactions chimiques spécifiques. Présente dans de nombreux écosystèmes océaniques, cette émission lumineuse joue des rôles écologiques variés : communication, défense, attraction ou camouflage. Cette rencontre propose de mieux comprendre les mécanismes scientifiques et les fonctions écologiques de la bioluminescence, tout en interrogeant la manière dont la découverte de ces formes de vie souvent invisibles peut nourrir l’émerveillement et renforcer la sensibilisation du public à la préservation de la biodiversité marine.

Avec : Jeremie Brugidou, artiste et chercheur ; Youri Timsit, Directeur de Recherche au CNRS ; et Gaël Clément , paléontologue au Muséum national d’Histoire naturelle.

Événement gratuit dans la limite des places disponibles – Réservation conseillée !
Les 30 premiers visiteurs auront droit à une boisson offerte !

Mercredi 15 avril – Bar des Sciences : Mondes marins sonores
Dédiée aux paysages sonores sous-marins, cette soirée nous plonge dans l’univers acoustique des océans et nous aide à comprendre ce que les sons révèlent de la santé des écosystèmes.

  • 18h30 – 19h | Apéro-quiz Océan

Un temps convivial animé par la Fondation de la Mer, pour explorer de manière ludique les mystères du monde marin.

  • 19h – 20h | Discussion croisée animée par Sophie Bécherel

Une rencontre entre artistes et chercheurs pour interroger l’impact des activités humaines sur l’environnement acoustique des océans et réfléchir à la manière dont l’écoute peut devenir un outil de connaissance, de protection et de relation au vivant .

Avec : Antoine Bertin, artiste sonore; Lucia Di Lorio, spécialiste des paysages sonores et de l’éco-acoustique appliquée à l’étude des dynamiques des écosystèmes marins et Aurore Morin, du Fonds international pour la protection des animaux (IFAW), chargée de la campagne “Vitesses Bleues” pour un océan plus silencieux.

Événement gratuit dans la limite des places disponibles – Réservation conseillée !
Les 30 premiers visiteurs auront droit à une boisson offerte !

Les structures océaniques (cyclones, anticyclones…) influencent le rôle des micro-organismes dans la séquestration du CO2 dans l’océan profond

by

L’océan joue un rôle majeur dans le cycle planétaire du carbone, en transformant une partie du CO2 atmosphérique en carbone organique grâce à la photosynthèse en utilisant l’énergie lumineuse des cent premiers mètres de l’océan. Une partie de ce carbone organique va être transformée avant de chuter par gravité des zones éclairées de l’océan vers les zones profondes sous forme de particules et d’agrégats également appelés neige marine. Ce flux de carbone et d’énergie alimente les écosystèmes profonds et permet une séquestration du carbone à plus ou moins long terme, selon la profondeur atteinte. La compréhension de ces mécanismes complexes, connus sous le nom de pompe biologique gravitationnelle, reliant la surface à l’océan profond, est essentielle à la modélisation du cycle du carbone global et donc aux projections climatiques à l’échelle de la planète.

Cette étude, publiée le 8 janvier, propose un changement de perspective pour comprendre le rôle des microbes dans le cycle du carbone océanique. Elle distingue deux groupes de micro-organismes, d’une part, les microbes en suspension, qui regroupent à la fois les micro-organismes libres dans l’eau et ceux attachés à des particules en suspension (qui ne coulent pas) ; et d’autre part, les micro-organismes attachés à la neige marine qui chute par gravité vers le fond de l’océan. Ces deux groupes jouent des rôles distincts et complémentaires dans le cycle du carbone de la zone mésopélagique des océans. Les micro-organismes en suspension maintiennent les stocks de carbone de la zone mésopélagique grâce à une fixation du carbone inorganique in-situ dans l’obscurité (dark carbon fixation, c’est-à-dire une production nouvelle de carbone organique à partir de carbone inorganique sans énergie lumineuse), tandis que les micro-organismes associés aux particules qui chutent dégradent la matière organique et régulent l’atténuation des flux de carbone particulaire en cours de sédimentation.

Cet article scientifique est le fruit d’une collaboration internationale pilotée par des scientifiques de l’Institut Méditerranéen d’Océanologie (MIO, CNRS/Aix-Marseille Université/IRD/Université de Toulon). Il est basé sur les données issues de la campagne océanographique APERO (Assessing marine biogenic matter Production, Export and Remineralization : from the surface to the dark Ocean), menée durant 45 jours dans l’Atlantique Nord en 2023, projet co-porté par Laurent Memery (LEMAR, CNRS, IFREMER, IRD, Université de Bretagne Occidentale, Brest), Lionel Guidi (LOV, CNRS, Sorbonne Université, Villefranche-sur-Mer) et Christian Tamburini (MIO), qui a mobilisé deux navires de la Flotte Océanographique Française et a permis d’échantillonner simultanément à travers différentes structures dynamiques (tourbillons cycloniques et anticycloniques, fronts cycloniques) à différentes profondeurs.

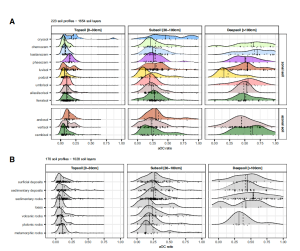
Pour mesurer la fixation du carbone inorganique dans l’obscurité (micro-organismes autotrophes) et l’activité métabolique des micro-organismes hétérotrophes (producteurs de carbone inorganique), les scientifiques ont adopté une approche innovante, combinant mesures de traceurs isotopiques et analyse génétique. Ils ont notamment utilisé une ligne de mouillage dérivante de 1 km de long (0 – 1000m), équipée de pièges à sédiment pour prélever les micro-organismes attachés aux particules qui sédimentent le long de la colonne d’eau.
 

En échantillonnant simultanément dans plusieurs zones hydrologiques contrastées, à différentes profondeurs, les chercheurs ont pu constater que :

  • Les micro-organismes attachés aux particules en cours de chute contribuent à 8–21 % de la demande totale en carbone, avec un rôle accru au niveau des fronts.
  • Ces processus varient fortement selon les structures physiques (cyclones, anticyclones, fronts), soulignant la nécessité d’intégrer la variabilité méso-échelle (tourbillonnaire) dans les modèles biogéochimiques.
  • Dans le tourbillon cyclonique, la fixation de carbone inorganique dans l’océan obscure par les micro-organismes en suspension représente jusqu’à 50 % des apports totaux en carbone organique, soit une contribution comparable à celle du flux de particules.

Ces découvertes permettent de réévaluer les flux de carbone dans l’océan profond et d’améliorer les modèles climatiques en prenant mieux en compte la zone mésopélagique et les structures physiques à méso-échelle. Cette étude représente une avancée majeure pour réduire les incertitudes sur le devenir du carbone dans l’océan et son impact sur le climat.